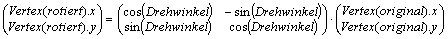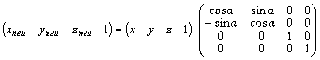In diesem Teil werden wir uns nun mit Matrizen befassen, und Sie werden erfahren, wie man mit ihrer Hilfe alle Transformationsschritte zu einer einzigen Gesamttransformation zusammenfassen kann.
Im Grunde könnte man meinen, Matrizen wurden erfunden, weil Mathematiker schreibfaule Menschen sind.
Betrachten wir noch einmal die Gleichungen für die Rotation um die z-Achse:
Vertex(rotiert).x = cos(Drehwinkel) * Vertex(original).x –
sin(Drehwinkel) * Vertex(original).y
Vertex(rotiert).y = sin(Drehwinkel) * Vertex(original).x +
cos(Drehwinkel) * Vertex(original).y
sin(Drehwinkel) * Vertex(original).y
Vertex(rotiert).y = sin(Drehwinkel) * Vertex(original).x +
cos(Drehwinkel) * Vertex(original).y
Mithilfe der so genannten Matrizen-Schreibweise lassen sich diese beiden Gleichungen wie folgt vereinfachen:
Matrizengleichung (Spaltenform)
Der Ausdruck
wird als 2x2-Matrix bezeichnet, da dieser aus zwei Zeilen und zwei Spalten besteht.
Entsprechend dieser Nomenklatur kann ein zweidimensionaler Zeilenvektor auch als 1x2-Matrix (1 Zeile, 2 Spalten) und ein zweidimensionaler Spaltenvektor als 2x1-Matrix (2 Zeilen, 1 Spalte) bezeichnet werden.
Durch Vergleich der ursprünglichen Transformationsgleichungen mit der Matrixgleichung wird ersichtlich, wie Matrix und Vektor miteinander multipliziert werden:
Hinweis:
Jede Zeile der Matrix wird komponentenweise mit dem Spaltenvektor (Vertex original) multipliziert, und die Produkte werden anschließend addiert (Merkregel: Zeile mal Spalte). Dabei ist zu beachten, dass die Anzahl der Komponenten von Zeile und Spalte miteinander übereinstimmen müssen. Selbige Multiplikationsregel haben wir bereits bei der Berechung von Skalarprodukten kennengelernt:
Eine Matrizengleichung kann gleichermaßen mithilfe von Spaltenvektoren oder Zeilenvektoren formuliert werden. Hier die Variante mit Zeilenvektoren zum direkten Vergleich:
Zunächst einmal fällt auf, dass sich die Multiplikationsreihenfolge geändert hat. Arbeitet man mit Spaltenvektoren, dann multipliziert man die Matrix mit dem Vektor, verwendet man Zeilenvektoren lautet die Reihenfolge Vektor mal Matrix. Diese Notwendigkeit ergibt sich direkt aus der Multiplikationsregel (die Anzahl der Komponenten von Zeile und Spalte müssen bei einer Multiplikation miteinander übereinstimmen).
Weiterhin fällt auf, dass die einzelnen Matrixelemente an der Hauptdiagonalen (Diagonale von links oben nach rechts unten) gespiegelt sind. Der Mathematiker spricht hier von einer transponierten Matrix.
Hinweis:
Im Rahmen der Spieleprogrammierung arbeitet man mit Matrizengleichungen in Zeilenform.
Da sich Vektoren als Spezialfälle von Matrizen auffassen lassen, können die Regeln der Vektoraddition, -subtraktion und skalaren Multiplikation eins zu eins auf Matrizen übertragen werden:
Subtraktion zweier Matrizen
Multiplikation zweier Matrizen
Die Translationsmatrix
Die Skalierungsmatrix
Haben alle Skalierungsfaktoren einen Wert von 1, dann wird die Skalierungsmatrix auch als Einheitsmatrix bezeichnet:
Rotation um die x-Achse
Rotation um die y-Achse
Rotation um die z-Achse
Rotation um eine beliebige Achse
Hinweis:
Mit Hilfe der inversen Matrix lässt sich die Transformation einer Matrix wieder rückgängig machen. Bewirkt eine Rotationsmatrix beispielsweise eine Drehung von 10° um die x-Achse, so bewirkt die inverse Rotationsmatrix eine Drehung von –10° um die gleiche Achse.
Dabei kennzeichnen x, y und z die Komponenten der normierten Rotationsachse.
Eine Matrix für die kombinierte Beschreibung von Skalierung, Rotation und Translation
Zum Abschluss dieses Artikels bleibt die Frage zu klären, wie man Skalierung, Rotation und Translation eines Spieleobjekts mithilfe einer einzigen Matrix beschreiben kann. Auf die praktische Umsetzung wird dann im nächsten Teil dieser Artikelserie eingegangen werden. An dieser Stelle sollen zunächst zwei Möglichkeiten zur Berechnung der Gesamttransformationsmatrix besprochen werden.
Möglichkeit 1:
Gesamttransformationsmatrix = Skalierungsmatrix*
Gesamtrotationsmatrix*
Translationsmatrix
Gesamtrotationsmatrix*
Translationsmatrix
Bitte beachten sie, dass Matrizen nicht einfach in einer beliebigen Reihenfolge miteinander multipliziert werden dürfen. Die Multiplikationsreihenfolge entspricht der Reihenfolge, wie die einzelnen Transformationsschritte ausgeführt werden müssen (Skalierung, Rotation und Translation).
Möglichkeit 2:
Gesamttransformationsmatrix = Skalierungsmatrix*
Gesamtrotationsmatrix
Gesamtrotationsmatrix
Anschließend müssen der Gesamttransformationsmatrix die Verschiebungen in x-, y- und z-Richtung zugewiesen werden:
Gesamttransformationsmatrix.41 = VerschiebungX
Gesamttransformationsmatrix.42 = VerschiebungY
Gesamttransformationsmatrix.43 = VerschiebungZ
Gesamttransformationsmatrix.42 = VerschiebungY
Gesamttransformationsmatrix.43 = VerschiebungZ